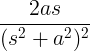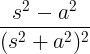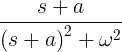Laplace Transform

Laplace transform converts a time domain function to s-domain function by integration from zero to infinity

 of the time domain function, multiplied by e-st.

The Laplace transform is used to quickly find solutions for differential equations and integrals.

Derivation in the time domain is transformed to multiplication by s in the s-domain.

Integration in the time domain is transformed to division by s in the s-domain.

Laplace transform function

The Laplace transform is defined with the L{} operator:

F(s)=\mathcal{L}\left \{ f(t)\right \}=\int_{0}^{\infty }e^{-st}f(t)dt

Inverse Laplace transform

The inverse Laplace transform can be calculated directly.

Usually the inverse transform is given from the transforms table.

Laplace transform table

Function name Time domain function Laplace transform

f (t)

F(s) = L{f (t)}
Constant 1 \frac{1}{s}
Linear t \frac{1}{s^2}
Power

t n

\frac{n!}{s^{n+1}}
Power

t a

Γ(a+1) ⋅ s -(a+1)
Exponent

e at

\frac{1}{s-a}
Sine

sin at

\frac{a}{s^2+a^2}
Cosine

cos at

\frac{s}{s^2+a^2}
Hyperbolic sine

sinh at

\frac{a}{s^2-a^2}
Hyperbolic cosine

cosh at

\frac{s}{s^2-a^2}
Growing sine

t sin at

\frac{2as}{(s^2+a^2)^2}
Growing cosine

t cos at

\frac{s^2-a^2}{(s^2+a^2)^2}
Decaying  sine

e -at sin ωt

\frac{\omega }{\left ( s+a \right )^2+\omega ^2}
Decaying cosine

e -at cos ωt

\frac{s+a }{\left ( s+a \right )^2+\omega ^2}
Delta function

δ(t)

1
Delayed delta

δ(t-a)

e-as

Laplace transform properties

Property name Time domain function Laplace transform Comment
 

f (t)

F(s)

  
Linearity a f (t)+bg(t) aF(s) + bG(s) a,b are constant
Scale change f (at) \frac{1}{a}F\left ( \frac{s}{a} \right ) a>0
Shift e-at f (t) F(s + a)  
Delay f (t-a) e-asF(s)  
Derivation \frac{df(t)}{dt} sF(s) - f (0)  
N-th derivation \frac{d^nf(t)}{dt^n} snf (s) - sn-1f (0) - sn-2f '(0)-...-f (n-1)(0)  
Power t n f (t) (-1)^n\frac{d^nF(s)}{ds^n}  
Integration \int_{0}^{t}f(x)dx \frac{1}{s}F(s)  
Reciprocal \frac{1}{t}f(t) \int_{s}^{\infty }F(x)dx  
Convolution f (t) * g (t) F(s) ⋅ G(s) * is the convolution operator
Periodic function f (t) = f (t+T) \frac{1}{1-e^{-sT}}\int_{0}^{T}e^{-sx}f(x)dx  

Laplace transform examples

Example #1

Find the transform of f(t):

f (t) = 3t + 2t2

Solution:

ℒ{t} = 1/s2

ℒ{t2} = 2/s3

F(s) = ℒ{f (t)} = ℒ{3t + 2t2} = 3ℒ{t} + 2ℒ{t2} = 3/s2 + 4/s3

 

Example #2

Find the inverse transform of F(s):

F(s) = 3 / (s2 + s - 6)

Solution:

In order to find the inverse transform, we need to change the s domain function to a simpler form:

F(s) = 3 / (s2 + s - 6) = 3 / [(s-2)(s+3)] = a / (s-2) + b / (s+3)

[a(s+3) + b(s-2)] / [(s-2)(s+3)] = 3 / [(s-2)(s+3)]

a(s+3) + b(s-2) = 3

To find a and b, we get 2 equations - one of the s coefficients and second of the rest:

(a+b)s + 3a-2b = 3

a+b = 0 , 3a-2b = 3

a = 3/5 , b = -3/5

F(s) = 3 / 5(s-2) - 3 / 5(s+3)

Now F(s) can be transformed easily by using the transforms table for exponent function:

f (t) = 3e2t - 3e-3t

 

See also

Contact Us

CALCULUS
ABOUT